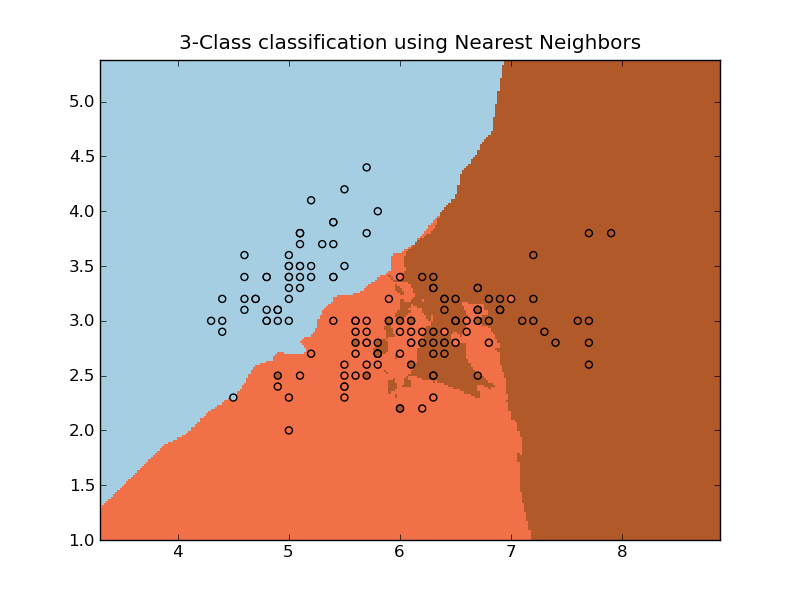
3.4. Nearest Neighbors

The principle behind nearest neighbor methods is to find the k training points closest in euclidean distance to x0, and then classify using a majority vote among the k neighbors.

Despite its simplicity, nearest neighbors has been successful in a large number of classification problems, including handwritten digits or satellite image scenes. It is ofter successful in situation where the decision boundary is very irregular.

3.4.1. Classification

The NeighborsClassifier implements the nearest-neighbors classification method using a vote heuristic: the class most present in the k nearest neighbors of a point is assigned to this point.

It is possible to use different nearest neighbor search algorithms by using the keyword algorithm. Possible values are 'auto', 'ball_tree', 'brute' and 'brute_inplace'. 'ball_tree' will create an instance of BallTree to conduct the search, which is usually very efficient in low-dimensional spaces. In higher dimension, a brute-force approach is prefered thus parameters 'brute' and 'brute_inplace' can be used . Both conduct a brute-force search, the difference being that 'brute_inplace' does not perform any precomputations, and thus is better suited for low-memory settings. Finally, 'auto' is a simple heuristic that will guess the best approach based on the current dataset.

Examples:

• Nearest Neighbors: an example of classification using nearest neighbor.

3.4.2. Regression

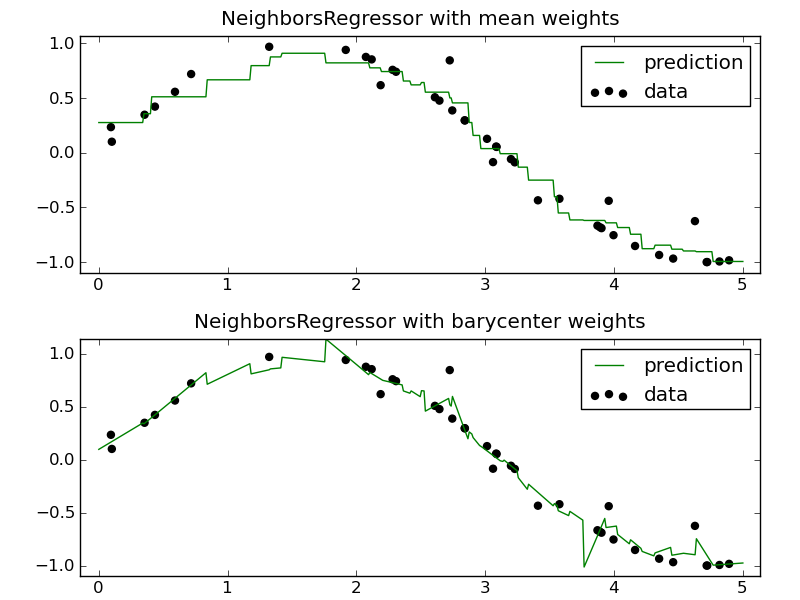
The NeighborsRegressor estimator implements a nearest-neighbors regression method by weighting the targets of the k-neighbors. Two different weighting strategies are implemented: barycenter and mean. barycenter will apply the weights that best reconstruct the point from its neighbors while mean will apply constant weights to each point. This plot shows the behavior of both classifier for a simple regression task.

Examples:

• k-Nearest Neighbors regression: an example of regression using nearest neighbor.

3.4.3. Efficient implementation: the ball tree

Behind the scenes, nearest neighbor search is done by the object BallTree. This algorithm makes it possible to rapidly look up the nearest neighbors in low-dimensional spaces.

This class provides an interface to an optimized BallTree implementation to rapidly look up the nearest neighbors of any point. Ball Trees are particularly useful for low-dimensional data and scales better than traditional tree searches (e.g. KD-Trees) as the number of dimensions grow. However, on high-dimensional spaces (dim > 50), brute force will eventually take on and become more efficient on such spaces.

Compared to a KDTree, the cost is a slightly longer construction time, though for repeated queries, this added construction time quickly becomes insignificant. A Ball Tree reduces the number of candidate points for a neighbor search through use of the triangle inequality:

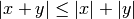
Each node of the BallTree defines a centroid, C, and a radius r such that each point in the node lies within the hyper-sphere of radius r, centered at C. With this setup, a single distance calculation between a test point and the centroid is sufficient to determine a lower bound on the distance to all points within the node. Carefully taking advantage of this property leads to determining neighbors in O[log(N)] time, as opposed to O[N] time for a brute-force search.

A pure C implementation of brute-force search is also provided in function knn_brute.

References:

• “Five balltree construction algorithms”, Omohundro, S.M., International Computer Science Institute Technical Report