Gaussian Mixture Model Sine Curve

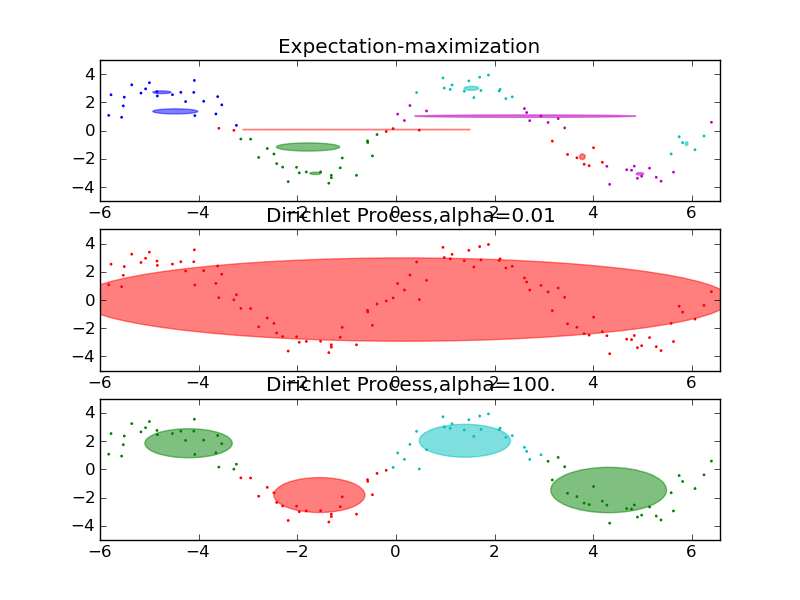
This example highlights the advantages of the Dirichlet Process: complexity control and dealing with sparse data. The dataset is formed by 100 points loosely spaced following a noisy sine curve. The fit by the GMM class, using the expectation-maximization algorithm to fit a mixture of 10 gaussian components, finds too-small components and very little structure. The fits by the dirichlet process, however, show that the model can either learn a global structure for the data (small alpha) or easily interpolate to finding relevant local structure (large alpha), never falling into the problems shown by the GMM class.

Python source code: plot_gmm_sin.py

import itertools

import numpy as np
from scipy import linalg
import pylab as pl
import matplotlib as mpl

from sklearn import mixture

# Number of samples per component
n_samples = 100

# Generate random sample following a sine curve
np.random.seed(0)
X = np.zeros((n_samples, 2))
step = 4*np.pi/n_samples

for i in xrange(X.shape[0]):
    x = i*step-6
    X[i,0] = x+np.random.normal(0, 0.1)
    X[i,1] = 3*(np.sin(x)+np.random.normal(0, .2))


color_iter = itertools.cycle (['r', 'g', 'b', 'c', 'm'])


for i, (clf, title) in enumerate([
        (mixture.GMM(n_components=10, cvtype='diag'), "Expectation-maximization"),
        (mixture.DPGMM(n_components=10, cvtype='diag', alpha=0.01),
         "Dirichlet Process,alpha=0.01"),
        (mixture.DPGMM(n_components=10, cvtype='diag', alpha=100.),
         "Dirichlet Process,alpha=100.")
        ]):

    clf.fit(X, n_iter=100)
    splot = pl.subplot(3, 1, 1+i)
    Y_ = clf.predict(X)
    for i, (mean, covar, color) in enumerate(zip(clf.means, clf.covars,
                                                 color_iter)):
        v, w = linalg.eigh(covar)
        u = w[0] / linalg.norm(w[0])
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y_ == i):
            continue
        pl.scatter(X[Y_== i, 0], X[Y_== i, 1], .8, color=color)

        # Plot an ellipse to show the Gaussian component
        angle = np.arctan(u[1]/u[0])
        angle = 180 * angle / np.pi # convert to degrees
        ell = mpl.patches.Ellipse(mean, v[0], v[1], 180 + angle, color=color)
        ell.set_clip_box(splot.bbox)
        ell.set_alpha(0.5)
        splot.add_artist(ell)

    pl.xlim(-6, 4*np.pi-6)
    pl.ylim(-5, 5)
    pl.title(title)

pl.show()