5.1. Cross-Validation¶
Learning the parameters of a prediction function and testing it on the
same data yields a methodological bias. To avoid over-fitting, we
have to define two different sets : a learning set 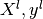 which is used for learning the prediction function (also called training
set), and a test set
which is used for learning the prediction function (also called training
set), and a test set 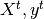 which is used for testing the
prediction function. However, by defining these two sets, we drastically
reduce the number of samples which can be used for learning the model,
and the results can depend on a particular couple of learning set
and test set.
which is used for testing the
prediction function. However, by defining these two sets, we drastically
reduce the number of samples which can be used for learning the model,
and the results can depend on a particular couple of learning set
and test set.
A solution is to split the whole data several consecutive times in different learning set and test set, and to return the averaged value of the prediction scores obtained with the different sets. Such a procedure is called cross-validation. This approach can be computationally expensive, but does not waste too much data (as it is the case when fixing an arbitrary test set), which is a major advantage in problem such as inverse inference where the number of samples is very small.
5.1.1. Computing cross-validated metrics¶
The simplest way to use perform cross-validation in to call the cross_val_score helper function on the estimator and the dataset.
The following example demonstrates how to estimate the accuracy of a linear kernel Support Vector Machine on the iris dataset by splitting the data and fitting a model and computing the score 5 consecutive times (with different splits each time):
>>> from sklearn import datasets
>>> from sklearn import svm
>>> from sklearn import cross_validation
>>> iris = datasets.load_iris()
>>> clf = svm.SVC(kernel='linear')
>>> scores = cross_validation.cross_val_score(
... clf, iris.data, iris.target, cv=5)
...
>>> scores
array([ 1. ..., 0.96..., 0.9 ..., 0.96..., 1. ...])
The mean score and the standard deviation of the score estimate are hence given by:
>>> print "Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() / 2)
Accuracy: 0.97 (+/- 0.02)
By default, the score computed at each CV iteration is the score method of the estimator. It is possible to change this by passing a custom scoring function, e.g. from the metrics module:
>>> from sklearn import metrics
>>> cross_validation.cross_val_score(clf, iris.data, iris.target, cv=5,
... score_func=metrics.f1_score)
...
array([ 1. ..., 0.96..., 0.89..., 0.96..., 1. ...])
In the case of the Iris dataset, the samples are balanced across target classes hence the accuracy and the F1-score are almost equal.
When the cv argument is an integer, cross_val_score uses the KFold or StratifiedKFold strategies by default (depending on the absence or presence of the target array).
It is also possible to use othe cross validation strategies by passing a cross validation iterator instead, for instance:
>>> n_samples = iris.data.shape[0]
>>> cv = cross_validation.ShuffleSplit(n_samples, n_iterations=3,
... test_fraction=0.3, random_state=0)
>>> cross_validation.cross_val_score(clf, iris.data, iris.target, cv=cv)
...
array([ 0.97..., 0.97..., 1. ])
The available cross validation iterators are introduced in the following.
5.1.2. Cross validation iterators¶
The following sections list utilities to generate boolean masks or indices that can be used to generate dataset splits according to different cross validation strategies.
Boolean mask vs integer indices
Most cross validators support generating both boolean masks or integer indices to select the samples from a given fold.
When the data matrix is sparse, only the integer indices will work as expected. Integer indexing is hence the default behavior (since version 0.10).
You can explicitly pass indices=False to the constructor of the CV object (when supported) to use the boolean mask method instead.
5.1.2.1. K-fold¶
KFold divides all the samples in math:K groups of samples,
called folds (if  , this is equivalent to the Leave One
Out strategy), of equal sizes (if possible). The prediction function is
learned using
, this is equivalent to the Leave One
Out strategy), of equal sizes (if possible). The prediction function is
learned using  folds, and the fold left out is used for test.
folds, and the fold left out is used for test.
Example of 2-fold:
>>> import numpy as np
>>> from sklearn.cross_validation import KFold
>>> X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
>>> Y = np.array([0, 1, 0, 1])
>>> kf = KFold(len(Y), 2, indices=False)
>>> print kf
sklearn.cross_validation.KFold(n=4, k=2)
>>> for train, test in kf:
... print train, test
[False False True True] [ True True False False]
[ True True False False] [False False True True]
Each fold is constituted by two arrays: the first one is related to the training set, and the second one to the test set. Thus, one can create the training/test sets using:
>>> X_train, X_test, y_train, y_test = X[train], X[test], Y[train], Y[test]
If X or Y are scipy.sparse matrices, train and test need to be integer indices. It can be obtained by setting the parameter indices to True when creating the cross-validation procedure:
>>> X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
>>> Y = np.array([0, 1, 0, 1])
>>> kf = KFold(len(Y), 2, indices=True)
>>> for train, test in kf:
... print train, test
[2 3] [0 1]
[0 1] [2 3]
5.1.2.2. Stratified K-Fold¶
StratifiedKFold is a variation of K-fold, which returns stratified folds, i.e which creates folds by preserving the same percentage for each target class as in the complete set.
Example of stratified 2-fold:
>>> from sklearn.cross_validation import StratifiedKFold
>>> X = [[0., 0.],
... [1., 1.],
... [-1., -1.],
... [2., 2.],
... [3., 3.],
... [4., 4.],
... [0., 1.]]
>>> Y = [0, 0, 0, 1, 1, 1, 0]
>>> skf = StratifiedKFold(Y, 2)
>>> print skf
sklearn.cross_validation.StratifiedKFold(labels=[0 0 0 1 1 1 0], k=2)
>>> for train, test in skf:
... print train, test
[1 4 6] [0 2 3 5]
[0 2 3 5] [1 4 6]
5.1.2.3. Leave-One-Out - LOO¶
LeaveOneOut (or LOO) is a simple cross-validation. Each learning set is created by taking all the samples except one, the test set being the sample left out. Thus, for n samples, we have n different learning sets and n different tests set. This cross-validation procedure does not waste much data as only one sample is removed from the learning set:
>>> from sklearn.cross_validation import LeaveOneOut
>>> X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
>>> Y = np.array([0, 1, 0, 1])
>>> loo = LeaveOneOut(len(Y))
>>> print loo
sklearn.cross_validation.LeaveOneOut(n=4)
>>> for train, test in loo:
... print train, test
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]
5.1.2.4. Leave-P-Out - LPO¶
LeavePOut is very similar to Leave-One-Out, as it creates all the
possible training/test sets by removing  samples from the complete set.
samples from the complete set.
Example of Leave-2-Out:
>>> from sklearn.cross_validation import LeavePOut
>>> X = [[0., 0.], [1., 1.], [-1., -1.], [2., 2.]]
>>> Y = [0, 1, 0, 1]
>>> lpo = LeavePOut(len(Y), 2)
>>> print lpo
sklearn.cross_validation.LeavePOut(n=4, p=2)
>>> for train, test in lpo:
... print train, test
[2 3] [0 1]
[1 3] [0 2]
[1 2] [0 3]
[0 3] [1 2]
[0 2] [1 3]
[0 1] [2 3]
5.1.2.5. Leave-One-Label-Out - LOLO¶
LeaveOneLabelOut (LOLO) is a cross-validation scheme which holds out the samples according to a third-party provided label. This label information can be used to encode arbitrary domain specific stratifications of the samples as integers.
Each training set is thus constituted by all the samples except the ones related to a specific label.
For example, in the cases of multiple experiments, LOLO can be used to create a cross-validation based on the different experiments: we create a training set using the samples of all the experiments except one:
>>> from sklearn.cross_validation import LeaveOneLabelOut
>>> X = [[0., 0.], [1., 1.], [-1., -1.], [2., 2.]]
>>> Y = [0, 1, 0, 1]
>>> labels = [1, 1, 2, 2]
>>> lolo = LeaveOneLabelOut(labels)
>>> print lolo
sklearn.cross_validation.LeaveOneLabelOut(labels=[1, 1, 2, 2])
>>> for train, test in lolo:
... print train, test
[2 3] [0 1]
[0 1] [2 3]
Another common application is to use time information: for instance the labels could be the year of collection of the samples and thus allow for cross-validation against time-based splits.
5.1.2.6. Leave-P-Label-Out¶
LeavePLabelOut is similar as Leave-One-Label-Out, but removes
samples related to  labels for each training/test set.
labels for each training/test set.
Example of Leave-2-Label Out:
>>> from sklearn.cross_validation import LeavePLabelOut
>>> X = [[0., 0.], [1., 1.], [-1., -1.], [2., 2.], [3., 3.], [4., 4.]]
>>> Y = [0, 1, 0, 1, 0, 1]
>>> labels = [1, 1, 2, 2, 3, 3]
>>> lplo = LeavePLabelOut(labels, 2)
>>> print lplo
sklearn.cross_validation.LeavePLabelOut(labels=[1, 1, 2, 2, 3, 3], p=2)
>>> for train, test in lplo:
... print train, test
[4 5] [0 1 2 3]
[2 3] [0 1 4 5]
[0 1] [2 3 4 5]
5.1.2.7. Random permutations cross-validation a.k.a. Shuffle & Split¶
The ShuffleSplit iterator will generate a user defined number of independent train / test dataset splits. Samples are first shuffled and then splitted into a pair of train and test sets.
It is possible to control the randomness for reproducibility of the results by explicitly seeding the random_state pseudo random number generator.
Here is a usage example:
>>> ss = cross_validation.ShuffleSplit(5, n_iterations=3, test_fraction=0.25,
... random_state=0)
>>> len(ss)
3
>>> print ss
ShuffleSplit(5, n_iterations=3, test_fraction=0.25, indices=True, ...)
>>> for train_index, test_index in ss:
... print train_index, test_index
...
[1 3 4] [2 0]
[1 4 3] [0 2]
[4 0 2] [1 3]
ShuffleSplit is thus a good alternative to KFold cross validation that allows a finer control on the number of iterations and the proportion of samples in on each side of the train / test split.
5.1.2.8. Bootstrapping cross-validation¶
Bootstrapping is a general statistics technique that iterates the computation of an estimator on a resampled dataset.
The Bootstrap iterator will generate a user defined number of independent train / test dataset splits. Samples are then drawn (with replacement) on each side of the split. It furthermore possible to control the size of the train and test subset to make their union smaller than the total dataset if it is very large.
Note
Contrary to other cross-validation strategies, bootstrapping will allow some samples to occur several times in each splits.
>>> bs = cross_validation.Bootstrap(9, random_state=0)
>>> len(bs)
3
>>> print bs
Bootstrap(9, n_bootstraps=3, n_train=5, n_test=4, random_state=0)
>>> for train_index, test_index in bs:
... print train_index, test_index
...
[1 8 7 7 8] [0 3 0 5]
[5 4 2 4 2] [6 7 1 0]
[4 7 0 1 1] [5 3 6 5]
5.1.3. Cross validation and model selection¶
Cross validation iterators can also be used to directly perform model selection using Grid Search for the optimal hyperparameters of the model. This is the topic if the next section: Grid Search.
