FastICA on 2D point clouds¶
Illustrate visually the results of Independent component analysis (ICA) vs Principal component analysis (PCA) in the feature space.
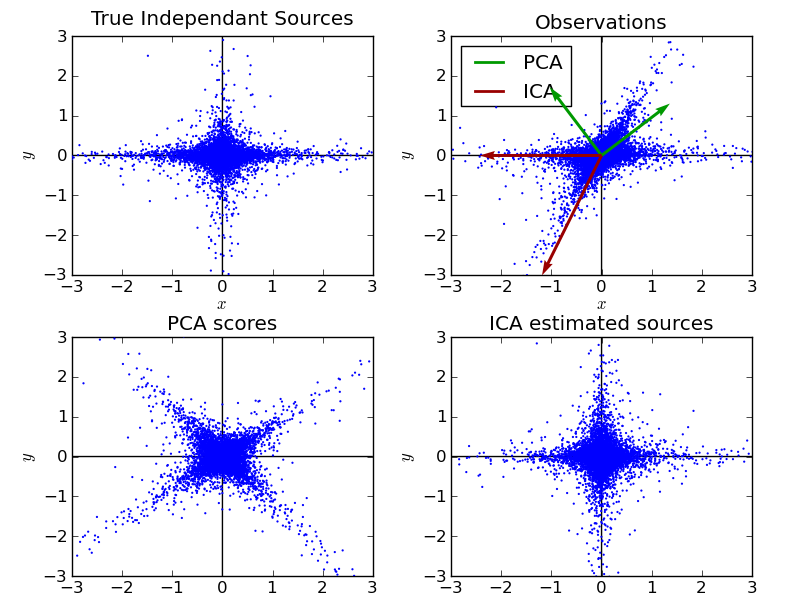
Representing ICA in the feature space gives the view of ‘geometric ICA’: ICA is an algorithm that finds directions in the feature space corresponding to projections with high non-Gaussianity. These directions need not be orthogonal in the original feature space, but they are orthogonal in the whitened feature space, in which all directions correspond to the same variance.
PCA, on the other hand, finds orthogonal directions in the raw feature space that correspond to directions accounting for maximum variance.
Here we simulate independent sources using a highly non-Gaussian process, 2 student T with a low number of degrees of freedom (top left figure). We mix them to create observations (top right figure). In this raw observation space, directions identified by PCA are represented by green vectors. We represent the signal in the PCA space, after whitening by the variance corresponding to the PCA vectors (lower left). Running ICA corresponds to finding a rotation in this space to identify the directions of largest non-Gaussianity (lower right).
Python source code: plot_ica_vs_pca.py
print __doc__
# Authors: Alexandre Gramfort, Gael Varoquaux
# License: BSD
import numpy as np
import pylab as pl
from scikits.learn.decomposition import PCA, FastICA
###############################################################################
# Generate sample data
S = np.random.standard_t(1.5, size=(2, 10000))
S[0] *= 2.
# Mix data
A = [[1, 1], [0, 2]] # Mixing matrix
X = np.dot(A, S) # Generate observations
pca = PCA()
S_pca_ = pca.fit(X.T).transform(X.T).T
ica = FastICA()
S_ica_ = ica.fit(X).transform(X) # Estimate the sources
S_ica_ /= S_ica_.std(axis=1)[:, np.newaxis]
###############################################################################
# Plot results
def plot_samples(S, axis_list=None):
pl.scatter(S[0], S[1], s=2, marker='o', linewidths=0, zorder=10)
if axis_list is not None:
colors = [(0, 0.6, 0), (0.6, 0, 0)]
for color, axis in zip(colors, axis_list):
axis /= axis.std()
x_axis, y_axis = axis
# Trick to get legend to work
pl.plot(0.1 * x_axis, 0.1 * y_axis, linewidth=2, color=color)
# pl.quiver(x_axis, y_axis, x_axis, y_axis, zorder=11, width=0.01,
pl.quiver(0, 0, x_axis, y_axis, zorder=11, width=0.01,
scale=6, color=color)
pl.hlines(0, -3, 3)
pl.vlines(0, -3, 3)
pl.xlim(-3, 3)
pl.ylim(-3, 3)
pl.xlabel('$x$')
pl.ylabel('$y$')
pl.subplot(2, 2, 1)
plot_samples(S / S.std())
pl.title('True Independant Sources')
axis_list = [pca.components_.T, ica.get_mixing_matrix()]
pl.subplot(2, 2, 2)
plot_samples(X / np.std(X), axis_list=axis_list)
pl.legend(['PCA', 'ICA'], loc='upper left')
pl.title('Observations')
pl.subplot(2, 2, 3)
plot_samples(S_pca_ / np.std(S_pca_, axis=-1)[:, np.newaxis])
pl.title('PCA scores')
pl.subplot(2, 2, 4)
plot_samples(S_ica_ / np.std(S_ica_))
pl.title('ICA estimated sources')
pl.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.26)
pl.show()
