PCA 2D projection of Iris dataset¶
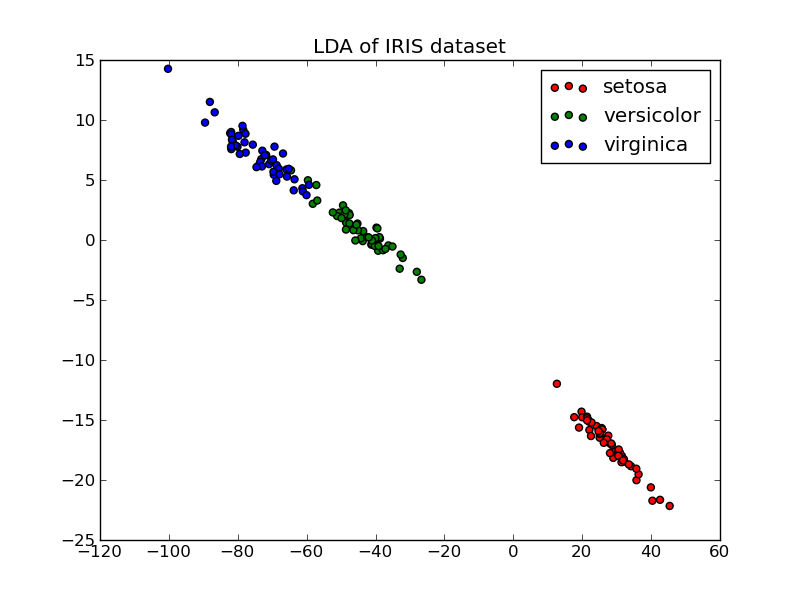
The Iris dataset represents 3 kind of Iris flowers (Setosa, Versicolour and Virginica) with 4 attributes: sepal length, sepal width, petal length and petal width.
Principal Component Analysis (PCA) applied to this data identifies the combination of attributes (principal components, or directions in the feature space) that account for the most variance in the data. Here we plot the different samples on the 2 first principal components.
Python source code: plot_pca_vs_lda.py
print __doc__
import pylab as pl
from scikits.learn import datasets
from scikits.learn.decomposition import PCA
from scikits.learn.lda import LDA
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)
lda = LDA(n_components=2)
X_r2 = lda.fit(X, y).transform(X)
# Percentage of variance explained for each components
print 'explained variance ratio (first two components):', \
pca.explained_variance_ratio_
pl.figure()
for c, i, target_name in zip("rgb", [0, 1, 2], target_names):
pl.scatter(X_r[y == i, 0], X_r[y == i, 1], c=c, label=target_name)
pl.legend()
pl.title('PCA of IRIS dataset')
pl.figure()
for c, i, target_name in zip("rgb", [0, 1, 2], target_names):
pl.scatter(X_r2[y == i, 0], X_r2[y == i, 1], c=c, label=target_name)
pl.legend()
pl.title('LDA of IRIS dataset')
pl.show()