4.5. Covariance estimation¶
Many statistical problems require at some point the estimation of a population’s covariance matrix, which can be seen as an estimation of data set scatter plot shape. Most of the time, such an estimation has to be done on a sample whose properties (size, structure, homogeneity) has a large influence on the estimation’s quality. The sklearn.covariance package aims at providing tools affording an accurate estimation of a population’s covariance matrix under various settings.
We assume that the observations are independent and identically distributed (i.i.d.).
4.5.1. Empirical covariance¶
The covariance matrix of a data set is known to be well approximated with the classical Maximum Likelihood Estimator (or empirical covariance), provided the number of observations is large enough compared to the number of features (the variables describing the observations). More precisely, the Maximum Likelihood Estimator of a sample is an unbiased estimator of the corresponding population covariance matrix.
The empirical covariance matrix of a sample can be computed using the empirical_covariance function of the package, or by fitting an EmpiricalCovariance object to the data sample with the EmpiricalCovariance.fit method. Be careful that depending whether the data are centered or not, the result will be different, so one may want to use the assume_centered parameter accurately.
Examples:
- See Ledoit-Wolf vs Covariance simple estimation for an example on how to fit an EmpiricalCovariance object to data.
4.5.2. Shrunk Covariance¶
4.5.2.1. Basic shrinkage¶
Despite being an unbiased estimator of the covariance matrix, the
Maximum Likelihood Estimator is not a good estimator of the
eigenvalues of the covariance matrix, so the precision matrix obtained
from its inversion is not accurate. Sometimes, it even occurs that the
empirical covariance matrix cannot be inverted for numerical
reasons. To avoid such an inversion problem, a transformation of the
empirical covariance matrix has been introduced: the shrinkage. It
consists in reducing the ratio between the smallest and the largest
eigenvalue of the empirical covariance matrix. This can be done by
simply shifting every eigenvalue according to a given offset, which is
equivalent of finding the l2-penalized Maximum Likelihood Estimator of
the covariance matrix, or by reducing the highest eigenvalue while
increasing the smallest with the help of a convex transformation :
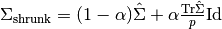 . The latter approach has been
implemented in scikit-learn.
. The latter approach has been
implemented in scikit-learn.
A convex transformation (with a user-defined shrinkage coefficient) can be directly applied to a pre-computed covariance with the shrunk_covariance method. Also, a shrunk estimator of the covariance can be fitted to data with a ShrunkCovariance object and its ShrunkCovariance.fit method. Again, depending whether the data are centered or not, the result will be different, so one may want to use the assume_centered parameter accurately.
Examples:
- See Ledoit-Wolf vs Covariance simple estimation for an example on how to fit a ShrunkCovariance object to data.
4.5.2.2. Ledoit-Wolf shrinkage¶
In their 2004 paper [1], O. Ledoit and M. Wolf propose a formula so as
to compute the optimal shrinkage coefficient 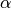 that
minimizes the Mean Squared Error between the estimated and the real
covariance matrix in terms of Frobenius norm.
that
minimizes the Mean Squared Error between the estimated and the real
covariance matrix in terms of Frobenius norm.
The Ledoit-Wolf estimator of the covariance matrix can be computed on a sample with the ledoit_wolf function of the sklearn.covariance package, or it can be otherwise obtained by fitting a LedoitWolf object to the same sample.
- [1] O. Ledoit and M. Wolf, “A Well-Conditioned Estimator for Large-Dimensional
- Covariance Matrices”, Journal of Multivariate Analysis, Volume 88, Issue 2, February 2004, pages 365-411.
Examples:
- See Ledoit-Wolf vs Covariance simple estimation for an example on how to fit a LedoitWolf object to data and for visualizing the performances of the Ledoit-Wolf estimator in terms of likelihood.
4.5.2.3. Oracle Approximating Shrinkage¶
Under the assumption that the data are Gaussian distributed, Chen et al. [2] derived a formula aimed at choosing a shrinkage coefficient that yields a smaller Mean Squared Error than the one given by Ledoit and Wolf’s formula. The resulting estimator is known as the Oracle Shrinkage Approximating estimator of the covariance.
The OAS estimator of the covariance matrix can be computed on a sample with the oas function of the sklearn.covariance package, or it can be otherwise obtained by fitting an OAS object to the same sample. The formula we used to implement the OAS does not correspond to the one given in the article. It has been taken from the MATLAB program available from the author’s webpage (https://tbayes.eecs.umich.edu/yilun/covestimation).
- [2] Chen et al., “Shrinkage Algorithms for MMSE Covariance Estimation”,
- IEEE Trans. on Sign. Proc., Volume 58, Issue 10, October 2010.
Examples:
- See Ledoit-Wolf vs Covariance simple estimation for an example on how to fit an OAS object to data.
- See Ledoit-Wolf vs OAS estimation to visualize the Mean Squared Error difference between a LedoitWolf and an OAS estimator of the covariance.
4.5.3. Sparse inverse covariance¶
The matrix inverse of the covariance matrix, often called the precision matrix, is proportional to the partial correlation matrix. It gives the partial independence relationship. In other words, if two features are independent conditionally on the others, the corresponding coefficient in the precision matrix will be zero. This is why it makes sense to estimate a sparse precision matrix: by learning independence relations from the data, the estimation of the covariance matrix is better conditioned. This is known as covariance selection.
In the small-samples situation, in which n_samples is on the order of magnitude of n_features or smaller, sparse inverse covariance estimators tend to work better than shrunk covariance estimators. However, in the opposite situation, or for very correlated data, they can be numerically unstable. In addition, unlike shrinkage estimators, sparse estimators are able to recover off-diagonal structure.
The GraphLasso estimator uses an l1 penalty to enforce sparsity on the precision matrix: the higher its alpha parameter, the more sparse the precision matrix. The corresponding GraphLassoCV object uses cross-validation to automatically set the alpha parameter.

A comparison of maximum likelihood, shrinkage and sparse estimates of the covariance and precision matrix in the very small samples settings.
Note
Structure recovery
Recovering a graphical structure from correlations in the data is a challenging thing. If you are interested in such recovery keep in mind that:
- Recovery is easier from a correlation matrix than a covariance matrix: standardize your observations before running GraphLasso
- If the underlying graph has nodes with much more connections than the average node, the algorithm will miss some of these connections.
- If your number of observations is not large compared to the number of edges in your underlying graph, you will not recover it.
- Even if you are in favorable recovery conditions, the alpha parameter chosen by cross-validation (e.g. using the GraphLassoCV object) will lead to selecting too many edges. However, the relevant edges will have heavier weights than the irrelevant ones.
The mathematical formulation is the following:
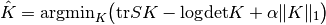
Where K is the precision matrix to be estimated, and S is the sample
covariance matrix. 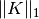 is the sum of the absolute values of
off-diagonal coefficients of K. The algorithm employed to solve this
problem is the GLasso algorithm, from the Friedman 2008 Biostatistics
paper. It is the same algorithm as in the R glasso package.
is the sum of the absolute values of
off-diagonal coefficients of K. The algorithm employed to solve this
problem is the GLasso algorithm, from the Friedman 2008 Biostatistics
paper. It is the same algorithm as in the R glasso package.
Examples:
- Sparse inverse covariance estimation: example on synthetic data showing some recovery of a structure, and comparing to other covariance estimators.
- Visualizing the stock market structure: example on real stock market data, finding which symbols are most linked.
References:
- Friedman et al, “Sparse inverse covariance estimation with the graphical lasso”, Biostatistics 9, pp 432, 2008
4.5.4. Robust Covariance Estimation¶
Real data set are often subjects to measurement or recording errors. Regular but uncommon observations may also appear for a variety of reason. Every observation which is very uncommon is called an outlier. The empirical covariance estimator and the shrunk covariance estimators presented above are very sensitive to the presence of outlying observations in the data. Therefore, one should use robust covariance estimators to estimate the covariance of its real data sets. Alternatively, robust covariance estimators can be used to perform outlier detection and discard/downweight some observations according to further processing of the data.
The sklearn.covariance package implements a robust estimator of covariance, the Minimum Covariance Determinant [3].
4.5.4.1. Minimum Covariance Determinant¶
The Minimum Covariance Determinant estimator is a robust estimator of a data set’s covariance introduced by P.J.Rousseuw in [3]. The idea is to find a given proportion (h) of “good” observations which are not outliers and compute their empirical covariance matrix. This empirical covariance matrix is then rescaled to compensate the performed selection of observations (“consistency step”). Having computed the Minimum Covariance Determinant estimator, one can give weights to observations according to their Mahalanobis distance, leading the a reweighted estimate of the covariance matrix of the data set (“reweighting step”).
Rousseuw and Van Driessen [4] developed the FastMCD algorithm in order to compute the Minimum Covariance Determinant. This algorithm is used in scikit-learn when fitting an MCD object to data. The FastMCD algorithm also computes a robust estimate of the data set location at the same time.
Raw estimates can be accessed as raw_location_ and raw_covariance_ attributes of a MinCovDet robust covariance estimator object.
- [3] P. J. Rousseeuw. Least median of squares regression.
- Am Stat Ass, 79:871, 1984.
- [4] A Fast Algorithm for the Minimum Covariance Determinant Estimator,
- 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS.
Examples:
- See Robust vs Empirical covariance estimate for an example on how to fit a MinCovDet object to data and see how the estimate remains accurate despite the presence of outliers.
- See Robust covariance estimation and Mahalanobis distances relevance to visualize the difference between EmpiricalCovariance and MinCovDet covariance estimators in terms of Mahalanobis distance (so we get a better estimate of the precision matrix too).
| Influence of outliers on location and covariance estimates | Separating inliers from outliers using a Mahalonis distance |
|---|---|
 |
 |


