2. Supervised learning: predicting an output variable from high-dimensional observations¶

The problem solved in supervised learning

Supervised learning consists in learning the link between two datasets: the observed data X, and an external variable y that we are trying to predict, usually called target or labels. Most often, y is a 1D array of length n_samples.

All supervised estimators in the scikit-learn implement a fit(X, y) method to fit the model, and a predict(X) method that, given unlabeled observations X, returns predicts the corresponding labels y.

Vocabulary: classification and regression

If the prediction task is to classify the observations in a set of finite labels, in other words to “name” the objects observed, the task is said to be a classification task. On the opposite, if the goal is to predict a continous target variable, it is said to be a regression task.

In the scikit-learn, for classification tasks, y is a vector of integers.

Note: See the Introduction to machine learning with Scikit-learn Tutorial for a quick run-through on the basic machine learning vocabulary used within Scikit-learn.

2.1. Nearest neighbor and the curse of dimensionality¶

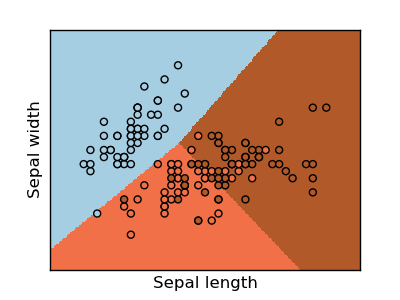
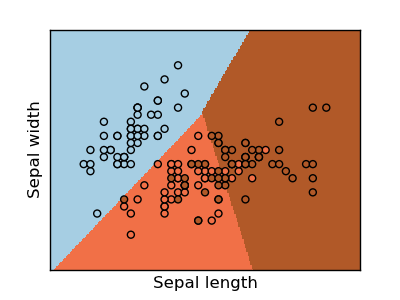
Classifying irises:

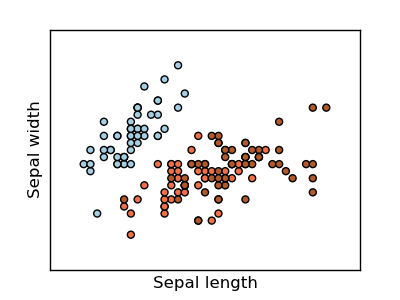
../../_images/plot_iris_dataset_3class_11.png

The iris dataset is a classification task consisting in identifying 3 different types of irises (Setosa, Versicolour, and Virginica) from their petal and sepal length and width:

>>> import numpy as np
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> iris_X = iris.data
>>> iris_y = iris.target
>>> np.unique(iris_y)
array([0, 1, 2])

2.1.1. k-Nearest neighbors classifier¶

The simplest possible classifier is the nearest neighbor: given a new observation x_test, find in the training set (i.e. the data used to train the estimator) the observation with the closest feature vector. (Please see the Nearest Neighbors section of the online Scikit-learn documentation for more information about this type of classifier.)

Training set and testing set

When experimenting with learning algorithm, it is important not to test the prediction of an estimator on the data used to fit the estimator, as this would not be evaluating the performance of the estimator on new data. This is why datasets are often split into train and test data.

KNN (k nearest neighbors) classification example:

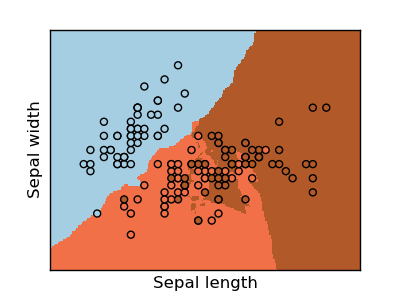
>>> # Split iris data in train and test data
>>> # A random permutation, to split the data randomly
>>> np.random.seed(0)
>>> indices = np.random.permutation(len(iris_X))
>>> iris_X_train = iris_X[indices[:-10]]
>>> iris_y_train = iris_y[indices[:-10]]
>>> iris_X_test  = iris_X[indices[-10:]]
>>> iris_y_test  = iris_y[indices[-10:]]
>>> # Create and fit a nearest-neighbor classifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> knn = KNeighborsClassifier()
>>> knn.fit(iris_X_train, iris_y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, n_neighbors=5,
       warn_on_equidistant=True, weights='uniform')
>>> knn.predict(iris_X_test)
array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])
>>> iris_y_test
array([1, 1, 1, 0, 0, 0, 2, 1, 2, 0])

2.1.2. The curse of dimensionality¶

If the data is only described by one feature, with values ranging from 0 to 1, with n train observations, new data will be no further away than 1/n and the nearest neighbor decision rule will be efficient as soon as 1/n is small compared to the scale of between-class feature variations.

If the number of features is p, the number of training samples to pave the [0, 1] space with a between-point distance of d, is 1/d**p. This number scales exponentialy p, the dimensionality of the problem.

In other words, the prediction problem becomes much harder for high-dimensional data. This is called the curse of dimensionality and is the core problem that machine learning addresses.

2.2. Linear model: from regression to sparsity¶

Diabetes dataset

The diabetes dataset consists of 10 physiological variables (age, sex, weight, blood pressure) measure on 442 patients, and an indication of disease progression after one year:

>>> diabetes = datasets.load_diabetes()
>>> diabetes_X_train = diabetes.data[:-20]
>>> diabetes_X_test  = diabetes.data[-20:]
>>> diabetes_y_train = diabetes.target[:-20]
>>> diabetes_y_test  = diabetes.target[-20:]

The task at hand is to predict disease prediction from physiological variables.

2.2.1. Linear regression¶

Linear regression, in it’s simplest form, fits a linear model to the data set by adjusting a set of parameters, in order to make the sum of the squared residuals of the model as small as possilbe.

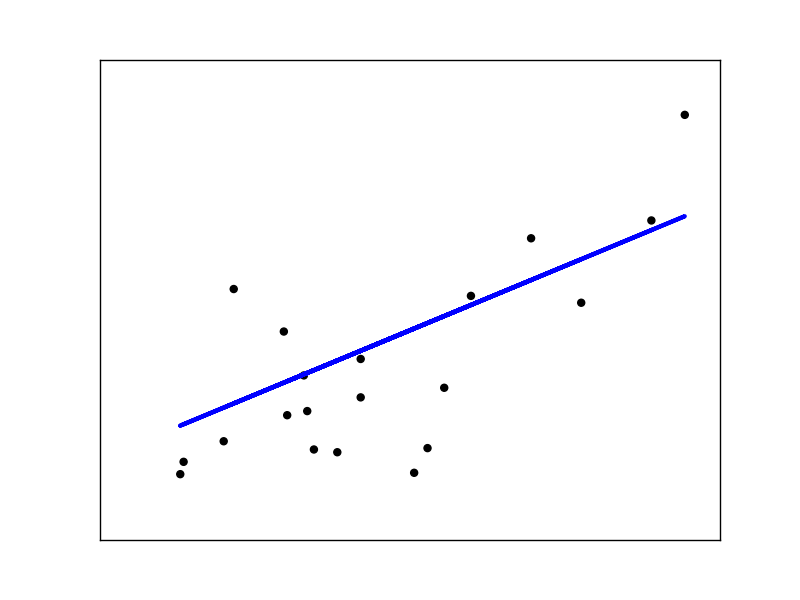
Linear models: 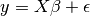$y = X\beta + \epsilon$

$X$ : data

$y$ : target variable

$\beta$ : Coefficients

$\epsilon$ : Observation noise

>>> from sklearn import linear_model
>>> regr = linear_model.LinearRegression()
>>> regr.fit(diabetes_X_train, diabetes_y_train)
LinearRegression(copy_X=True, fit_intercept=True, normalize=False)
>>> print regr.coef_
[  3.03499549e-01  -2.37639315e+02   5.10530605e+02   3.27736980e+02
  -8.14131709e+02   4.92814588e+02   1.02848452e+02   1.84606489e+02
   7.43519617e+02   7.60951722e+01]

>>> # The mean square error
>>> np.mean((regr.predict(diabetes_X_test) - diabetes_y_test)**2)
2004.5676026898223

>>> # Explained variance score: 1 is perfect prediction
>>> # and 0 means that there is no linear relationship
>>> # between X and Y.
>>> regr.score(diabetes_X_test, diabetes_y_test)
0.58507530226905713

2.2.2. Shrinkage¶

If there are few data points per dimension, noise in the observations induces high variance:

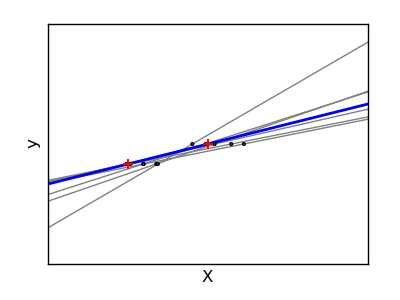
>>> X = np.c_[ .5, 1].T
>>> y = [.5, 1]
>>> test = np.c_[ 0, 2].T
>>> regr = linear_model.LinearRegression()

>>> import pylab as pl
>>> pl.figure() 

>>> np.random.seed(0)
>>> for _ in range(6): 
...    this_X = .1*np.random.normal(size=(2, 1)) + X
...    regr.fit(X, y)
...    pl.plot(test, regr.predict(test))
...    pl.scatter(this_X, y, s=3)

A solution, in high-dimensional statistical learning, is to shrink the regression coefficients to zero: any two randomly chosen set of observations are likely to be uncorrelated. This is called ridge regression:

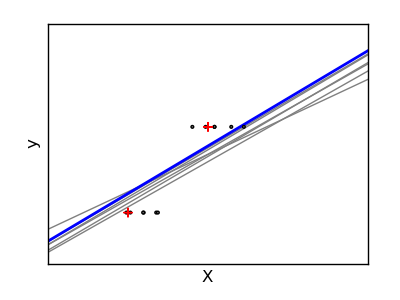
../../_images/plot_ridge_variance_11.png

>>> regr = linear_model.Ridge(alpha=.1)

>>> pl.figure() 

>>> np.random.seed(0)
>>> for _ in range(6): 
...    this_X = .1*np.random.normal(size=(2, 1)) + X
...    regr.fit(this_X, y)
...    pl.plot(test, regr.predict(test))
...    pl.scatter(this_X, y, s=3)

This is an example of bias/variance tradeoff: the larger the ridge alpha parameter, the higher the bias and the lower the variance.

We can choose alpha to minimize left out error, this time using the diabetes dataset, rather than our synthetic data:

>>> alphas = np.logspace(-4, -1, 6)
>>> print [regr._set_params(alpha=alpha
...             ).fit(diabetes_X_train, diabetes_y_train,
...             ).score(diabetes_X_test, diabetes_y_test) for alpha in alphas]
[0.58511106838835292, 0.58520730154446743, 0.58546775406984897, 0.58555120365039137, 0.58307170855541623, 0.570589994372801]

Note

Capturing in the fitted parameters noise that prevents the model to generalize to new data is called overfitting. The bias introduced by the ridge regression is called a regularization.

2.2.3. Sparsity¶

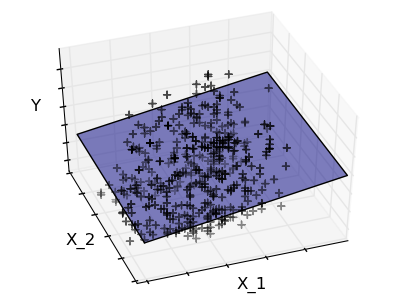
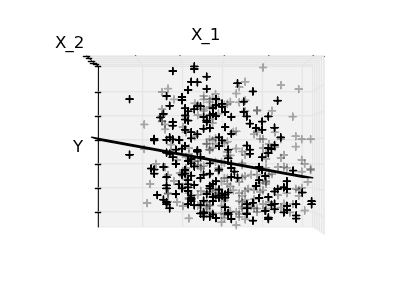
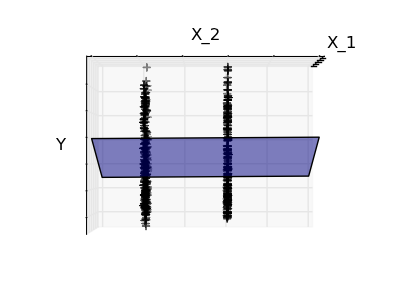
Fitting only features 1 and 2

Note

A representation of the full diabetes dataset would involve 11 dimensions (10 feature dimensions, and one of the target variable). It is hard to develop an intuition on such representation, but it may be useful to keep in mind that it would be a fairly empty space.

We can see that although feature 2 has a strong coefficient on the full model, it conveys little information on y when considered with feature 1.

To improve the conditioning of the problem (mitigate the The curse of dimensionality), it would be interesting to select only the informative features and set non-informative ones, like feature 2 to 0. Ridge regression will decrease their contribution, but not set them to zero. Another penalization approach, called Lasso (least absolute shrinkage and selection operator), can set some coefficients to zero. Such methods are called sparse method, and sparsity can be seen as an application of Occam’s razor: prefer simpler models.

>>> regr = linear_model.Lasso(alpha=.1)
>>> print [regr._set_params(alpha=alpha
...             ).fit(diabetes_X_train, diabetes_y_train
...             ).score(diabetes_X_test, diabetes_y_test)
...        for alpha in alphas]
[0.5851191069162196, 0.58524713649060311, 0.58571895391793782, 0.58730094854527282, 0.5887622418309254, 0.58284500296816755]

>>> best_alpha = alphas[4]
>>> regr.alpha = best_alpha
>>> regr.fit(diabetes_X_train, diabetes_y_train)
Lasso(alpha=0.025118864315095794, copy_X=True, fit_intercept=True,
   max_iter=1000, normalize=False, precompute='auto', tol=0.0001)
>>> print regr.coef_
[   0.         -212.43764548  517.19478111  313.77959962 -160.8303982    -0.
 -187.19554705   69.38229038  508.66011217   71.84239008]

Different algorithms for a same problem

Different algorithms can be used to solve the same mathematical problem. For instance the Lasso object in the scikit-learn solves the lasso regression using a coordinate decent method, that is efficient on large datasets. However, the scikit-learn also provides the linear_model.LassoLars object, using the LARS which is very efficient for problems in which the weight vector estimated is very sparse, that is problems with very few observations.

2.2.4. Classification¶

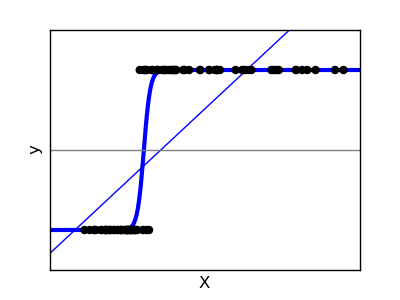
For classification, as in the labeling iris task, linear regression is not the right approach, as it will give too much weight to data far from the decision frontier. A linear approach is to fit a sigmoid function, or logistic function:

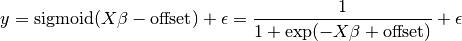
$y = \textrm{sigmoid}(X\beta - \textrm{offset}) + \epsilon = \frac{1}{1 + \textrm{exp}(- X\beta + \textrm{offset})} + \epsilon$

>>> logistic = linear_model.LogisticRegression(C=1e5)
>>> logistic.fit(iris_X_train, iris_y_train)
LogisticRegression(C=100000.0, dual=False, fit_intercept=True,
          intercept_scaling=1, penalty='l2', tol=0.0001)

Multiclass classification

If you have several classes to predict, an option often used is to fit one-versus-all classifiers, and use a voting heuristic for the final decision.

Shrinkage and sparsity with logistic regression

The C parameter controls the amount of regularization in the LogisticRegression object, the bigger C, the less regularization. penalty=”l2” gives Shrinkage (i.e. non-sparse coefficients), while penalty=”l1” gives Sparsity.

Excercise

Try classifying the digits dataset with nearest neihbors and a linear model. Leave out the last 10% and test prediction performance on these observations.

2.2.4.1. Excercice: classification of digits

2.3. Support vector machines (SVMs)¶

2.3.1. Linear SVMs¶

The SVM is a discrimant model: they try to find a combination of samples to build a plane maximizing the margin between the two classes. Regularization is set by the C parameter: the small the choice of C, means a stronger regularization, which means the margin will be caluculated using many, to all the observations around the separation line; a larger choice of C will thus have the margins computed on the observations that are close to the separating line.

Unregularized SVM	Regularized SVM (default)

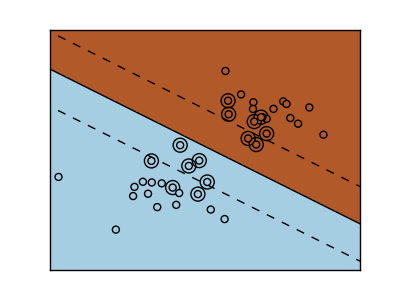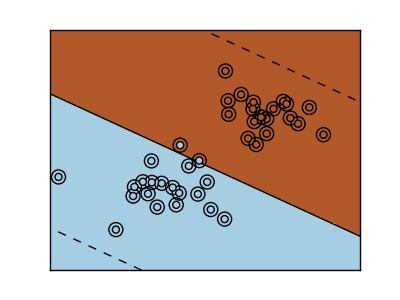SVMs can be used in regression –SVR (Support Vector Regression)–, or in classification –SVC (Support Vector Classification).

>>> from scikits.learn import svm
>>> svc = svm.SVC(kernel='linear')
>>> svc.fit(iris_X_train, iris_y_train)
SVC(C=1.0, cache_size=200, coef0=0.0, degree=3, gamma=0.0, kernel='linear',
  probability=False, shrinking=True, tol=0.001)

Warning

Normalizing data

For many estimators, including the SVMs, having datasets with unit standard deviation for each feature is important to get good prediction.

2.3.2. Using kernels¶

Classes are not always separable in feature space. The solution is to build a decision function that is not linear but that may be for instance polynomial. This is done using the kernel trick that can be seen as creating an decision energy by positioning kernels on observations:

Linear kernel	Polynomial kernel

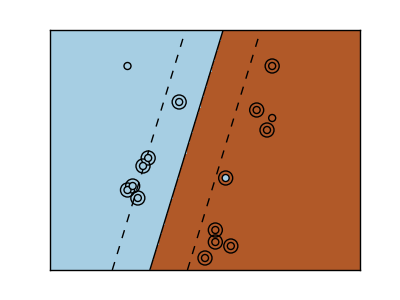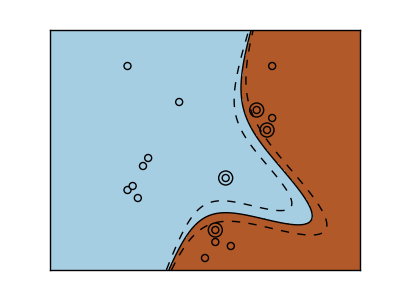>>> svc = svm.SVC(kernel='linear')	>>> svc = svm.SVC(kernel='poly', ... degree=3) >>> # degree: polynomial degree

RBF kernel (Radial Basis Function)

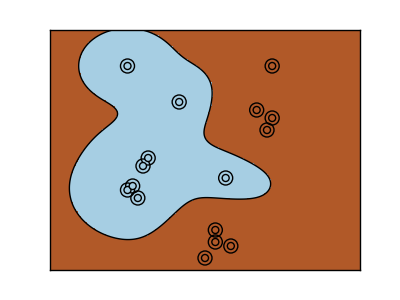>>> svc = svm.SVC(kernel='rbf')
>>> # gamma: inverse of size of
>>> # radial kernel

Interactive example

See the SVM GUI to download svm_gui.py; add data points of both classes with right and left button, fit the model and change parameters and data.

Excercise

Try classifying classes 1 and 2 from the iris dataset with SVMs, with the 2 first features. Leave out 10% of each class and test prediction performance on these observations.

The solution is available below:

2.3.2.1. Excercice: classification of iris

Warning: the classes are ordered, do not leave out the last 10%, you would be testing on only one class.

Hint: You can use the decision_function method on a grid to get intuitions.

Citing

This page